要点
-
原子時計の多様な時刻ゆらぎを評価する新たな指標として高階アラン分散を提案
-
高階アラン分散を原子時計の時刻ゆらぎを特徴づける分散パラメータの関数として表現する公式を発見
-
次世代無線通信Beyond 5G/6Gに不可欠なモバイル端末や無線基地局間の高精度時刻同期に貢献
東京工業大学 工学院 システム制御系の石崎孝幸准教授、市村太一大学院生、群馬大学大学院理工学府 電子情報部門の川口貴弘助教、国立研究開発法人情報通信研究機構(NICT)電磁波研究所の矢野雄一郎主任研究員、花土ゆう子協力研究員の研究グループは、原子時計の多様な時刻ゆらぎを評価するために、高階アラン分散と呼ばれる指標を新たに定義して、その合理性を数学的に解析するとともに、高階アラン分散を原子時計の時刻ゆらぎを特徴づける分散パラメータの関数として記述する普遍的な公式を発見した。
次世代無線通信規格Beyond 5G/6Gでは、モバイル端末や無線基地局間の時刻同期精度を向上することが通信の高速・大容量化、高信頼・低遅延化、多接続化に直結する。特に、モバイル端末の高精度時刻同期を実現するためのキーデバイスとして、小型原子時計の研究開発が活発に行われている。原子時計は原子固有の遷移周波数を基準とすることにより、現在主流の水晶時計と比較して桁違いに正確な時刻を刻むことが可能である。しかしながら、原子時計にもわずかな時刻のゆらぎが生じる。時刻ゆらぎの統計的性質には、原子時計の内部構造や原子遷移の検出方法などの複数の要素が影響するため、原子時計の多様な時刻ゆらぎを統一的に評価する指標が求められていた。
本研究では、形状や仕組みが異なるさまざまな種類の原子時計にも汎用的に適用可能な時刻ゆらぎの評価指標をシステム制御の数理に基づいて解析した。本研究が明らかにした高階アラン分散の数学的な性質と関数表現は、原子時計の性能評価にとどまらず、精密計測に関わる計量学分野全般の基礎となることも期待される。
本成果は、2023年12月20日(現地時間)に、計量学分野の権威ある国際学術誌である「Metrologia」に掲載された。
背景
世界各国で研究開発が進められている次世代無線通信規格Beyond 5G/6Gでは、現在の5Gを超える通信の高速・大容量化、高信頼・低遅延化、多接続化の実現を目指している。これらの目標を達成するためには、複数のモバイル端末や無線基地局が協調することが必要とされており、モバイル端末や無線基地局間のより高精度な時刻同期技術を開発することが重要である。高精度時刻同期は、正確な売買時刻の管理が必要とされる金融商取引、高度な需給電力制御が必要なスマートグリッド、高精度な測位が必要とされる自動運転やロボット・ドローン制御などの我々の社会生活を支えるインフラにも欠かせない。
高精度時刻同期を支えるキーデバイスの一つは原子時計である。原子時計は、現在主流の水晶時計と比較して桁違いに正確な時刻を刻むことができる。しかしながら、原子時計にもわずかな時刻ゆらぎが生じる。時刻ゆらぎの統計的性質は原子時計の種類や個体差によって異なるため、時刻ゆらぎの統計的性質を解析して、個々の原子時計の性能を合理的に評価することが重要である。搭載する原子時計の性能は、モバイル端末や無線基地局の間で達成可能な時刻同期精度に直結するため、時刻同期に基づくインフラの信頼性を担保するためにも時刻ゆらぎの解析は欠かせない。特に、長年の運用によって特性が分かっている従来の原子時計だけでなく、開発段階にあって特性が定まっていない小型原子時計に対しても、時刻ゆらぎの統計的性質を適切に評価することが求められる。
研究成果
1. 既存の評価指標とその課題
時刻ゆらぎの統計的性質は、主に原子時計の種類に応じた「次数」とゆらぎの振幅に関わる「分散パラメータ」によって定まる。例えば、原子時計の次数が「2」であることは、時刻ゆらぎの成分として、白色ガウス雑音を時間に関して1回積分した成分と、2回積分した成分の「2種類」が含まれることを指す。分散パラメータは、2つの雑音成分それぞれに対する倍率を表す。一般に、次数nの原子時計の時刻ゆらぎには、n個の分散パラメータで規定される雑音成分が含まれる。同じ種類の原子時計であっても分散パラメータが同じであるとは限らず、個々の原子時計のゆらぎの大きさには個体差がある。
原子時計の時刻ゆらぎを解析する最も標準的な指標はアラン分散である。アラン分散の歴史は古く、基本となるアイディアの提唱は1966年に遡る。アラン分散を原子時計の計測データに対して計算することにより、各雑音成分の倍率である分散パラメータが推定できる。分散パラメータの推定には、各雑音成分が支配的となる時間スケールに差があることを利用する。
図1左に、次数が2の原子時計2つに対してアラン分散を計算した数値シミュレーション例を示す。縦軸は時刻ゆらぎの大きさ、横軸は分散を計算する時間スケールを表す。例えば、横軸のτ=100(102)秒の点でのアラン分散の値は、その原子時計の刻む時刻が100秒間でどの程度ゆらぐかを示している。図1左では、時刻ゆらぎが計測のたびに確率的に変化することを考慮して、各々の原子時計に対して48回の計測を行った場合におけるアラン分散の曲線を重ねて描画している。各原子時計に対して計算された48本のアラン分散の曲線が重なっていることから、計測データの確率的な変化によらず、アラン分散の曲線はほとんど変化していないことが分かる。また、すべてのτにおいてBの曲線がAの曲線よりも下側にあることから、短期的にも長期的にも原子時計Bの時刻ゆらぎがAよりも小さいことが分かる。このように、アラン分散によって、次数が2である原子時計の時刻ゆらぎを解析することができる。なお、次数2の原子時計の例として、セシウム原子時計などが長年の運用によって知られている。
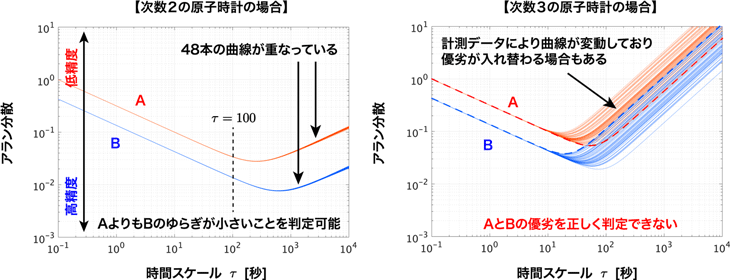
図1:次数2の原子時計(左)と次数3の原子時計(右)のアラン分散の曲線(原子時計AよりもBの時刻ゆらぎが小さい)
一方、図1右は次数3の原子時計に対してアラン分散を同様に計算した例である。こちらの例では、約10(101)秒以上の時間スケールにおけるアラン分散の曲線が、計測データによって変動していることが分かる。また、破線のように、2つの原子時計に対するアラン分散の大小が計測データによって入れ替わる場合もある。したがって、統計的に十分な回数の計測を繰り返さない限り、特に長期的な時刻精度について、2つの原子時計の優劣を判定することができない。この例が示すように、次数が3である原子時計の場合には、計測のたびにアラン分散の曲線が大きく変動してしまう。なお、次数3の原子時計の例として、水素メーザー原子時計が知られている。
次数が3以下の原子時計の精度は、アラン分散に代えてアダマール分散と呼ばれる指標によって解析が可能である。図2は上述したものと同じ次数2と3の原子時計に対してアダマール分散を計算した例である。計測データによらずアダマール分散の曲線は不変であることから、どちらの種類の原子時計に対しても1回の計測だけで精度を特定できることが分かる。
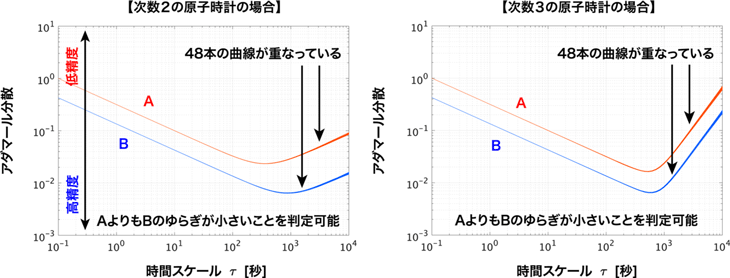
図2:次数2の原子時計(左)と次数3の原子時計(右)のアダマール分散の曲線(原子時計AよりもBの時刻ゆらぎが小さい)
しかしながら、アラン分散やアダマール分散によって1回の計測で原子時計の精度を正しく特定するためには、その原子時計の次数が既知であることが前提となる点に注意が必要である。言い換えれば、次数が未知の新しい種類の原子時計では、1回の計測で精度を正しく特定できる保証がない。例えば、原子時計の次数が4であることを知らずにアダマール分散を計算すると、図3左のように原子時計の優劣を正しく判定できない。このことが、上述した既存指標を用いて新しい原子時計の時刻ゆらぎを解析する場合の課題となっていた。また、次数が未知の原子時計では、複数の既存指標を適切に換算することができなかった。このため、計測データから得られた複数の指標値を合理的に比較できないことも課題となっていた。
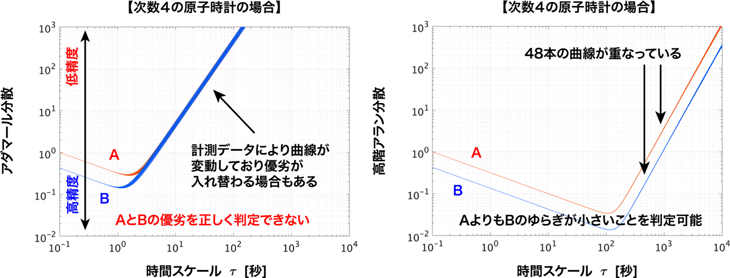
図3:次数4の原子時計に対するアダマール分散(左)と高階アラン分散(右)の曲線(原子時計AよりもBの時刻ゆらぎが小さい)
2. 高階アラン分散の提案
本研究では、これら2つの課題を解決する新たな指標として「高階アラン分散」を新たに定義して、数学的性質をシステム制御の数理に基づいて解析した。その結果、任意の次数の原子時計に適用可能な高階アラン分散を分散パラメータの関数として表す公式を発見した。図4にその公式を示す。

図4:高階アラン分散を原子時計の分散パラメータの関数で表す公式
原子時計の次数はn、分散パラメータはq1,...,qnで表されている。本研究の数理解析によって、高階アラン分散の階数Nが原子時計の次数n以上であるとき、またそのときに限って、図4に示される時間依存項が零となることが分かった。この時間依存項が存在しなければ、計測データによらず高階アラン分散の曲線は変動しない。このことから、どのような次数の原子時計であっても、十分に大きな階数を選ぶことによって、高階アラン分散の曲線が計測のたびに変動しないことが結論づけられる。端的に言えば、原子時計の次数が未知であったとしても、時刻ゆらぎの大きさを1回の計測で適切に評価できる。 図3右は次数4の原子時計に対して、階数4の高階アラン分散によって時刻ゆらぎの大きさを評価した例である。
また、本研究が導出した公式は、既存指標を含むすべての階数の高階アラン分散を合理的に比較することも可能にしている。具体的には、高階アラン分散の定義は、階数Nを2に選ぶと通常のアラン分散の定義に、3に選ぶとアダマール分散の定義に一致する。さらに、階数Nを4以上に選ぶ場合には、既存指標を一般化した新たな指標となる。高階アラン分散の公式は、原子時計のゆらぎを特徴づける分散パラメータの関数として、階数が異なる指標値の関係を明示している。
社会的インパクト
近年では、世界各国における開発競争によって、原子時計の小型化、省電力化、高性能化が格段に進んでいる。Beyond 5G/6Gが普及した近未来には、チップスケールの原子時計をスマートフォンなどの身近なモバイル端末に搭載することも想定されている。自動運転やロボット・ドローン制御の他にも高精度測位を活用した新たなサービスが登場することにより、原子時計の活用範囲は地上に基地局をもつモバイル通信網を超えて、月や火星などにおける探査機のナビゲーションにも広がることが期待されている。
本研究が提案する高階アラン分散は、特性が分かっている従来の原子時計だけでなく、特性が分かっていない小型原子時計の精度も適切に評価することができる。さまざまな原子時計の精度を正しく評価することは、高精度時刻同期に基づくシステムやサービスの信頼性と性能の向上につながる。例えば、高精度測位サービスでは、時刻同期の精度が位置情報の正確さに直結することから、時刻同期精度を向上することによって、ロボットやドローンによる運送の安全性と効率性が高められる。
「時間」はSI単位系の中で最も高精度で計測が可能な物理量である。「長さ」が真空中の光速と時間によって定義されているように、時刻を正確に計測することは、国際的な計量標準の制定にも深く関わる。原子時計の時刻ゆらぎを評価する基本指標となる高階アラン分散は、精密計測に関わる計量学分野での応用も期待される。
今後の展開
近年では、世界各国でさまざまな種類の小型原子時計の研究が進んでいる。マッチ箱サイズの商用小型原子時計をさらに低コスト化、低消費電力化する研究や、蒸気化されたアルカリ原子による原子ビーム時計やルビジウム原子による光時計などの研究が代表的である。また、直鎖型分子を用いた分子時計や水銀イオンを電場で閉じ込めるイオントラップ時計など、原子だけではなく分子やイオンを活用した新方式も登場している。今後は、これらの新しい種類の原子時計を高階アラン分散に基づいて解析することによって、統計的な観点から個々の原子時計が持つ時刻ゆらぎの特性を明らかにしていくことを目指す。
各機関の役割分担
- 東京工業大学:システム制御理論に基づく高階アラン分散の数理解析。
- 群馬大学:小型時計原子時計モデルの数理解析のための事前解析・評価、初期検討。
- 情報通信研究機構:小型原子時計の時刻ゆらぎに関する課題提起、計測技術の見地による解析結果の解釈。
付記
本研究は、総務省の「電波資源拡大のための研究開発による委託研究(JPJ000254)」により実施された。
論文情報
掲載誌:Metrologia
論文タイトル:Higher-Order Allan Variance for Atomic Clocks of Arbitrary Order: Mathematical Foundation
著者:Takayuki Ishizaki, Taichi Ichimura, Takahiro Kawaguchi, Yuichiro Yano, Yuko Hanado
DOI:10.1088/1681-7575/ad02fe
 sc.e.titech.ac.jp
sc.e.titech.ac.jp