トップページ > 組織紹介 > 未来ICT研究所 > 量子ICT先端開発センター > 研究テーマ > 量子情報理論
情報技術は「ものを識別する」という能力の上に立って、 効率的に情報を表現し、それを正確に伝送・処理するということで 成り立っています。ものの識別は信号検出という問題として、また、 情報の効率的な表現は情報源符号化、そして情報の正確な伝送は 通信路符号化という問題として定義され、これらが情報科学の主要課題を 構成しています。量子力学まで枠を広げた場合、これらの問題がどのように 一般化されるのか、また、量子効果を活かすことで可能になる新しい 伝送・処理方式の能力と限界がどこにあるのか等を明らかにして行くのが 量子情報理論です。
一方、こうした量子情報の基礎理論は抽象的な理論であり、 物理的にどのように実現すればよいのかという設計理論は、まだ多くのことが 明らかになっていません。我々は量子情報理論と、主に光によるその実現化の 設計理論について、次の３つの課題に分けて研究を進めています。
主担当者： 佐々木 雅英、武岡 正裕
我々が日常的に扱う「情報記号」を、量子限界にさらされた通信路を通して 伝送するという問題は、量子情報理論の基本的なテーマの一つです。 ここでは、量子状態の信号をどのような戦略で検出するのか、検出に必要な量子測定過程を如何に実現するか、そしてこのような 量子信号検出を駆使した情報処理である量子符号化について研究しています。
量子力学的物体の取る状態（量子状態）を如何に識別するか、究極の識別限界がどのように決まっているか、に関する問題です。ビットエラーレートを下げたい のか、符号の識別性を高めたいのか、より複雑なパターン構造を識別したいのか等々、目的によって最適な量子信号検出の方法は異なります。ここでは最適な信 号検出を実現するための量子測定過程について、できるだけ物理的実現法を示唆できるような最適解の導出を中心に研究を進めています。
＜代表的論文＞
・量子一括測定について：
M. Sasaki et al.,
Phys. Rev. A 58, 159 (1998); LANL quant-ph/9801012.
・相互情報最適測定について:
M. Sasaki et al.,
Phys. Rev. A 59, 3325 (1999); LANL quant-ph/9812062.
・量子パターンマッチングについて:
M. Sasaki and A. Carlini,
Phys. Rev. A 66, 022303 (2002); LANL quant-ph/0202173.
・最適位相評価とその実現法について:
M. Sasaki, A. Carlini, and A. Chefles,
J. Phys. A: Math. Gen. 34, 7017 (2001); LANL quant-ph/0011057.
・量子暗号の盗聴戦略に関する測定法について:
C. A. Fuchs and M. Sasaki,
Quant. Inf. Comput. 3(5), 377 (2003); LANL quant-ph/0107024.
このように目的に応じて数学的に量子導出された次の問題は、数式で与えられた量子測定を物理的にどのように実現するのかが課題となります。ここでは、ビー ムスプリッターなどの線形光学素子と、当研究室で開発中である光子検出器を用いた場合に、原理的にどのようなクラスの量子測定が実現可能であるのかを明ら かにする基礎設計理論の構築を目指しています。
＜代表的論文＞
・連続測定と光子検出器を用いた量子測定の設計法について:
M. Takeoka, M. Sasaki, P. van Loock, and N. Luetkenhaus,
Phys. Rev. A. 71, 022318 (2005); LANL quant-ph/0410133.
量子情報源符号化
量子状態を使って如何に効率良く情報を表現するかと言う問題です。具体的には、データの圧縮に関連した問題です。 （詳細は「通信の基本原理」を参照）
量子通信路符号化
量子状態を使って如何に正確に情報を伝送するかと言う問題です。 具体的には、誤り訂正に関連した問題です。 （詳細は「通信の基本原理」を参照）
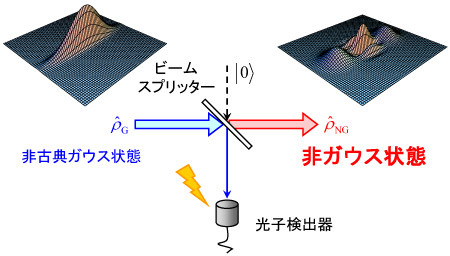
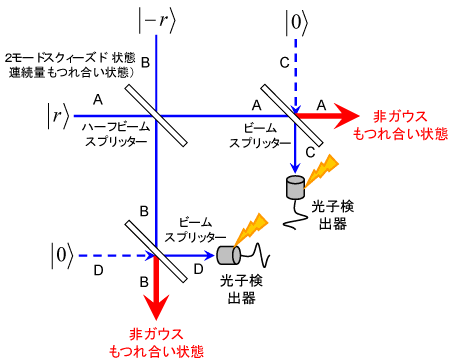
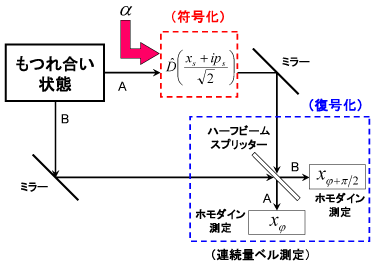
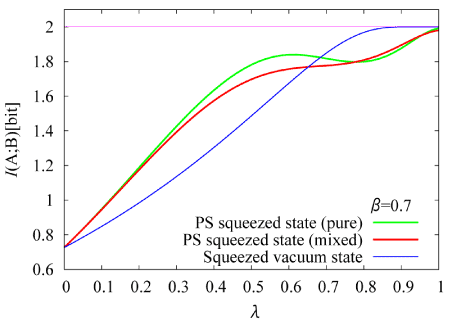
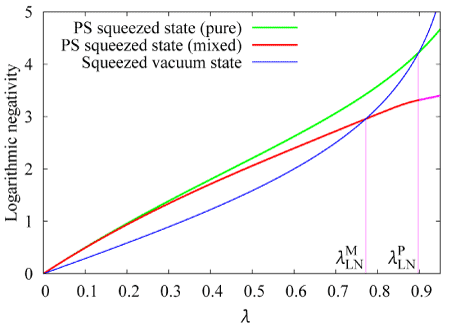
量 子もつれ状態とは、例えば分子のスピンシングレット状態のように複数の構成要素からなる量子系特有の相関を持つ状態です。歴史的にはEinstein、 PodolskyとRosenがもしこのような状態を巨視的なスケールで実現できたとすると、これまでの古典物理学の直観ではでは解釈し切れない奇妙な結 果が生じてしまうとしてEinstein-Podolsky-Rosenのパラドックスとして長年にわたって議論されて来ました。しかし、実際そのような 奇妙な現象が量子力学の予言通り起こり、さらには従来の情報技術には類似のない転送技術や暗号技術、信号処理技術へ応用できることが分かって来ました。こ れまで原子スケールに特有の現象であった量子もつれ状態は、今や数10km以上離れた通信スケールまで展開できるようになって来ました。このような古典的 対応を持たない新たな通信資源を使った情報技術の研究も行っています。ここでは、２モードスクィーズド状態と呼ばれる量子もつれを使った量子情報処理プロ トコルに関して理論的な研究を進めています。この状態は波動関数がガウス分布で拡がるためガウス状態と呼ばれ、光の直交振幅と呼ばれる連続スペクトルを持 つ物理量に基づいた量子もつれ状態を形成しており、この状態は理論的にも実験的にも比較的扱いやすいクラスの状態です（実験に関しては「量子相関光子状態 制御」を参照）。２モードスクィーズド状態を用いた量子テレポーテーションや、量子もつれ支援計測技術について理論的な解析を行っています。
＜代表的論文＞
・雑音下における量子テレポーテーションについて:
M. Takeoka, M. Ban, and M. Sasaki,
J. Opt. B 4, 114 (2002); LANL quant-ph/0110031.
・量子テレポーテーションの通信路としてのモデル化について:
M. Ban, M. Sasaki, and M. Takeoka,
J. Phys. A: Math. Gen. 35, L401 (2002); LANL quant-ph/0202172.
・量子もつれ支援計測技術について:
M. Sasaki, M. Ban, and S. M. Barnett,
Phys. Rev. A 66, 022303 (2002); LANL quant-ph/0203113.
・量子もつれ支援計測技術について:
M. Takeoka, M. Ban, and M. Sasaki,
Phys. Rev. A. 68, 012307 (2003); LANL quant-ph/0304032.
現 在の光通信では，ノイズに対して頑強なガウス型の光を用いています．しかしガウス状態のみで量子計算を行ったとしても，その処理速度は高々古典計算機でも 到達しうる程度であることが知られています．またガウス状態のもつれ合い状態に対して，線形光学素子，スクィージング，ホモダイン測定などのガウス操作に よる局所変換を行ったとしても，もつれ合いを増強することは不可能です．そこで，量子情報処理において，その真の醍醐味を生かすには，ガウス型でない変換 を行うことが本質的な要素になる考えられます．非ガウス操作は３次以上のハミルトニアンで記述されますが，任意の非ガウス操作と適当なガウス操作を組み合 わせれば，原理的には任意の高次のハミルトニアンが実現出来ることが知られており，非ガウス操作の実用化は，普遍的な量子ゲート実現のために必要不可欠で あるといえます．
非ガウス型の操作としては，スクィージングと光子数測定を組み合わせた３次の位相ゲートなど測定誘起型のものや，４次の位相ゲート（カー効果）などが知ら れていますが，これらは複雑であったり，相互作用が弱すぎたりと，現時点でその効果を検証するためには適当ではないと考えられます．そこで我々はビームス プリッターと光子検出器を組み合わせた，さらに簡単な非ガウス操作を採用しています（図１）．入力状態の一部をビームスプリッターで切り分け，これを光子 検出器で測定，クリックした場合のみを選択的に取り出す，条件付き測定を行います．その結果，出力状態はいわゆる「シュレディンガーの猫状態」のような非 ガウス状態に射影されます（シルエットがガウス曲線でなくなっています）．
また，２モードスクィーズド状態はもつれ合い状態を実現していますが，同じく測定誘起型非ガウス操作を行う（図２）と，もつれ合いが増強されていることを 示唆する報告がこれまでになされています．我々は，非ガウスもつれ合い状態を用いると，量子稠密符号化通信路（図３）における相互情報量は，従来のス クィーズド状態の場合と比べて改善されることを明らかにしました（図４，λはスクィージングの強さ）．
さらに我々は，非ガウス状態のもつれ合いを直接的に評価するため，対数ネガティヴィティと呼ばれる測度の観点から解析を 行いました．この測度はもつれ合いに対して単調性を示すことに加え，混合状態の場合に対しても線形代数パッケージを用いることで計算が可能である，という 特徴があります．数値解析の結果，現状で到達可能なスクィージングの領域において，非ガウス操作を行った後では対数ネガティヴィティが大きくなっており （図５），非ガウス操作によりもつれ合いの度合いが確かに増加しうると結論づけることができます．
＜代表的論文＞
・非ガウス操作によるエンタングルメントの増強とデンスコーディングへの
応用について:
A. Kitagawa, M. Takeoka, K. Wakui, and M. Sasaki,
Phys. Rev. A 72, 022334 (2005); LANL quant-ph/0503049.
・対数ネガティヴィティによる非ガウスもつれ合い状態の評価について:
A. Kitagawa, M. Takeoka, M. Sasaki, and A. Chefles,
quant-ph/0512069 (2005)
