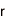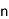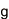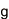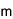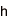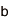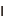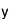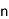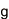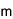将来にわたり情報漏えいの危険のない分散ストレージシステムの実証に成功

～パスワードを分散し情報理論的に安全な認証方式を実現～

2016年7月1日

国立研究開発法人情報通信研究機構
国立大学法人東京工業大学

ポイント

分散ストレージシステムにおいて認証・伝送・保存のすべてに情報理論的安全性の担保を実証
パスワード認証を用いた情報理論的に安全な認証方式を実現
将来どんなに計算機が発達しても情報漏えいの危険のない安全な分散ストレージを開発

NICT 量子ICT先端開発センター及びセキュリティ基盤研究室は、国立大学法人東京工業大学（東工大、学長: 三島良直）工学院情報通信系の尾形わかは教授と共同で、分散ストレージシステムにおいて認証・伝送・保存の過程をすべて情報理論的安全性で担保されるシステムの実証実験に世界で初めて成功しました。

NICTが運用している量子鍵配送（QKD）ネットワーク（名称: Tokyo QKD Network）を利用し、情報理論的に安全なデータ保存を可能とする分散ストレージプロトコルを実装しました。さらに、我々独自のプロトコルであり、一つのパスワードだけで情報理論的に安全なユーザ認証を可能とするパスワード分散プロトコルも併せて実装しました。

なお、この成果は、英国科学誌「Scientific Reports」（Nature Publishing Group）（電子版: 英国時間7月1日（金）午前10:00）に掲載される予定です。

本研究開発の一部は、総合科学技術・イノベーション会議により、制度設計された革新的研究開発推進プログラム（ImPACT）の支援を受けています。

背景

元NSA・CIA職員のスノーデン氏によるリーク情報でも喧伝されていますが、インターネットで使用されている暗号の一部は、既に破られている可能性があります。現在インターネット上で広く使用されている暗号の多くは、計算機による解読に膨大な時間を必要とすることを安全性の根拠としています。一方で、年々計算機の能力は向上しており、その安全性は日々低下していく宿命にあります。長期の秘匿性を必要とする情報、例えば30年後に漏えいしても大きな問題となる国家安全保障情報やゲノム情報等もインターネットを行き来し、保管される時代において、計算機の性能向上に安全性を脅かされない、将来にわたり安全性を保証できる情報伝送・保存システム（分散ストレージシステム）を確立することが急務となっています。

今回の成果

図1 情報理論的安全性を持つ分散ストレージ概念図

今回、情報理論的に安全なデータ保存を可能とする秘密分散法の代表的な方式である Shamir(シャミア)の(k,n)しきい値秘密分散法を用いた分散ネットワークをNICTが運用している量子鍵配送（QKD）ネットワーク上に実装し、さらに、NICT・東工大独自のプロトコルである利便性・操作性に優れたパスワード分散プロトコルを同時に実装し、分散ストレージに重要な3つのプロセスであるユーザ認証・伝送・保存のプロセスにおいて情報理論的に安全な分散システムの実証に成功しました。

QKDリンクは、二者間に安全に乱数を共有させることを可能とし、ワンタイムパッド暗号と組み合わせることにより、情報理論的に安全に通信できるシステムです。NICTは、2010年から敷設ファイバ網上に構築された様々なQKDリンクの相互接続を可能とし、鍵リレー等を管理しながらネットワーク上の任意の二者に安全に鍵を供給できるQKD Platformというレイヤアーキテクチャを開発し、実際のQKDネットワークを東京圏でTokyo QKD Networkとして運用しています。

Shamirの(k,n)しきい値秘密分散法は、情報理論的に安全にデータ保管を可能とするプロトコルとして知られており、この二つを組み合わせることにより、将来にわたり情報漏えいのない安全な分散ストレージを実現することができます。

一方、データを保存・復元する際のユーザ認証において情報理論的な安全性を満たし、かつ利便性・操作性に優れた方式は知られていませんでした。例えば Wegman-Carter認証方式は、安全にユーザ認証を可能としますが、大量の鍵を個人で管理する必要があり、専用のデバイスを必要とします。しかしながら、このことは鍵管理デバイスの紛失や鍵データの複製という危険性があることを意味し、デバイス管理を個人の責任において行わなければならないという不便さを伴います。

そこで、我々は一つのパスワードを用いて、情報理論的に安全なユーザ認証方式を新たに開発しました。通常のパスワード認証では計算量的な安全性しかなく、強力な計算機を用いればパスワードを推定される可能性がありました。それに対し、パスワード分散という新しいプロトコルを導入し、データを保存する本人は一つのパスワードを覚えているだけで、将来にわたり安全に認証できる方式を開発しました（補足資料図2参照）。

この方式実現には、通常の秘密データの分散と比較して、10倍以上のデータをストレージサーバ間で通信する必要があり、それに伴い、信頼性が高く高度に設計されたQKDネットワークが必須となります。今回我々は、分散ストレージを構成する3つのプロセス（ユーザ認証・伝送・保存）において情報理論的に安全なシステムを東京圏に敷設されたファイバ網上のQKDネットワークを用いて実証に成功しました。

今後の展望

今後は、さらに、分散ストレージの処理能力の向上を図り、より大量のデータを高速に処理できるシステムにするとともに、ネットワークの可用性を長期にわたり検証することで、実利用に耐え得るシステムの開発を進めていきます。また、本システムを用いた安全なデータ中継等の新しい応用の開発を進めていきます。

論文情報

掲載誌：Scientific Reports（Nature Publishing Group）, DOI: 10.1028/srep28988）

掲載論文名：Unbreakable distributed storage with quantum key distribution network and password-authenticated secret sharing

著者名：Mikio Fujiwara, Atsushi Waseda, Ryo Nojima, Shiho Moriai, Wakaha Ogata, and Masahide Sasaki

各機関の役割分担

NICT：プロトコル提案・証明と実証実験
東工大：プロトコル安全性証明

補足資料

図2 Tokyo QKD Network上に構築された分散ストレージシステム

STS(storage server): ストレージサーバ, KMS (key management server): 鍵管理サーバ
KMA (key management agent): 鍵管理エージェント, KSA (key supply agent): 鍵供給エージェント

今回の実験で使われている技術

量子鍵配送（QKD）を用いた完全秘匿通信（量子暗号）：
QKDによる暗号鍵の共有と、それを用いたワンタイムパッド暗号化を行うことにより、完全秘匿通信が可能になる。

図3 量子鍵配送を用いた完全秘匿通信の概要

信頼できる鍵中継ノード：
QKDシステムの信号媒体が単一光子であり、ファイバ内の損失で容易に消失してしまうこと及び単一光子検出を行う技術が非常に難しいことから、現在のQKDシステムの性能は、距離50kmで数百kbps程度でしかない。鍵を共有する距離を伸張するためには、50kmごとに秘密が漏えいすることのない中継ノードを設置して鍵をリレーする方法がある。この堅牢な安全性を持つ中継局のことを信頼できる中継ノードと呼称する。例えばA-B間のQKDリンクで生成した鍵をK1、B-C間QKD装置で生成した鍵をK2とする。A-C間で鍵を共有するにはBから排他的論理和(K1㊉K2)を古典情報としてCに送る。CではK2を知っているのでK1㊉K2㊉K2=K1となり、A-C間で鍵K1を共有できる。

QKDシステム内の鍵管理のためのレイヤ構造（図2参照）：
QKDにより生成された暗号鍵は、物理的に厳重に管理された場所に配置され、上位の鍵管理レイヤの鍵管理エージェントに吸い上げられる。鍵管理エージェント（Key management agent: KMA）は、暗号鍵と各リンクの鍵の量を常に把握し、鍵の量やリンクの状況を、更にその上の鍵管理サーバ（Key management server: KMS）に知らせる。鍵供給エージェント（Key supply agent: KSA）は使用アプリケーションに合わせ、QKDネットワークの任意の2点間に鍵を供給する。何時・何のアプリケーションに鍵を供給したかという情報は鍵管理サーバへ知らせる。

用語解説

量子鍵配送（QKD）: Quantum Key Distribution

量子鍵配送では、送信者が光子を変調（情報を付加）して伝送し、受信者は届いた光子1個1個の状態を検出し、盗聴の可能性のあるビットを排除（いわゆる鍵蒸留）して、絶対安全な暗号鍵（暗号化のための乱数列）を送受信者間で共有する。変調を施された光子レベルの信号は、測定操作をすると必ずその痕跡が残り、この原理を利用して盗聴を見破る。

元の記事へ

スノーデン氏によるリーク情報

日本語による解説記事
http://www.fortinet.co.jp/security_blog/130906-NSAs-and-GCHQ-Decryption-Capabilities.html
https://agilecatcloud.com/2015/10/20/researchers-claim-to-have-solved-nsa-crypto-breaking-mystery/

元の記事へ

Shamir(シャミア)の(k,n)しきい値秘密分散法

(k,n)しきい値秘密分散法では、最初に、秘密情報S（整数）の保有者がSからn個のシェアと呼ばれる値を生成する。

次に、秘密保有者は、シェア保有者（1～n）に各シェアを秘密裏に渡す。秘密保有者は、この後、秘密情報を消去する。

秘密情報の復元には、k人のシェア保有者が協力してk個のシェアを収集し、所定の計算をすることにより、秘密データSを復元できる。このときkをしきい値と定義する。

代表的な(k,n)しきい値法であるShamirの(k,n)しきい値秘密分散法は、以下のように構成される。

分散: 定数項を秘密情報Sとするランダムなk-1次多項式

f(x)=a_k-1x^k-1+…+ a₁x+a₀

を生成する。ここで、a_k-1,…, a₁はランダムな整数であり、a₀が秘密データSである。

シェア保有者の識別子をiとしたとき、シェア保有者にはシェアとして(i, f(i))を配布する。

復元時、k人のシェア保有者が(i, f(i))を持ち寄ることにより、a₀=Sを求める。

秘密情報Sの復元は、下記の式に従って行う。復元に協力するk人のシェア保有者の識別子を{i₁,…,i_k}とする。このとき、各シェア保有者の保有するシェアについて、

f(i₁)=a_k-1i₁^k-1+…+a₁i₁+a₀

…

f(i_k)=a_k-1i_k^k-1+…+a₁i_k+a₀

が成り立つ。ここで、(i₁, f(i₁)),…,(i_k, f(i_k))が与えられれば、未知変数をa_k-1,…,a₀のk個とするk変数1次方程式がk個与えられる。したがって、この連立方程式より、すべての未知変数を求めることが可能であり、秘密情報Sを復元できる。

実際に秘密情報を復元する際には、ラグランジュ補間が利用される。

下記は、(3,4)の例である。2次方程式中の3つの変数を確定するために、3組以上の(i, f(i))があれば、秘密データSを復元できる。

Shamir(シャミア)の(k,n)しきい値秘密分散法

元の記事へ

ワンタイムパッド暗号化

送信する情報（平文）のデジタルデータと同じ長さの真性乱数を暗号鍵として用意し、はぎ取り式メモ（パッド）のように1回ごとに使い捨てる暗号化方式。異なる平文ごとに、異なる暗号鍵を使う。平文と暗号鍵の排他的論理和によって暗号文を生成して伝送し、受信側で再び暗号文と暗号鍵の排他的論理和によって平文を復号する。この暗号化方式は、どんなに高い計算能力を持つ盗聴者であっても、暗号文から平文を永遠に解読できないことが証明されている最も安全で強固な暗号方式である。

元の記事へ

Wegman-Carter認証

最後に2者間で通信した内容を記録し、事前に共有している鍵を用いてダイジェストを作成する。次に、通信を開始する際に、お互いのダイジェストを送り合い、これが正しいことを確認することにより、相互認証を行う。認証ごとに新しい鍵を使用する。

元の記事へ