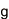現在の情報通信システムは、電磁気学や光学などの古典力学に基づいて設計されていますが、情報操作のルールを更に量子力学まで拡張することにより、従来不可能だった新機能、例えば、盗聴不可能な暗号通信(量子暗号)や究極的な低電力・大容量通信(量子通信)が可能になります。しかし、信号の量子力学的性質は回線内の損失や雑音によってすぐに壊れてしまうため、長距離化は容易ではありません。量子暗号の長距離化や量子通信の実現には、光信号の量子力学的性質を保ったまま、その振幅を増幅する技術が必要になります。さらに、雑音の混入もほぼ完全に防ぐ必要があります。しかし、従来の光増幅技術では、雑音の混入は原理的に避けられず、量子力学的性質を保ったまま光信号を増幅することは不可能でした。
独立行政法人 情報通信研究機構(以下「NICT」、理事長: 坂内 正夫)は、ソウル国立大学と共同で、量子暗号などで使われる微弱な光信号を、遠く離れた地点に大きな信号として増幅して再生する新しい方法を考案し、その実証に成功しました。これは、受信側にあらかじめ大きな振幅を持つ「量子重ね合わせ状態」という特殊な光を用意しておき、そこへ送りたい光信号の情報を転写するもので、雑音の混入が避けられない従来の光増幅器とは異なり、無雑音の信号増幅が可能です。量子暗号を長距離化できるほか、量子コンピュータの回路の構築にも使える新プロトコルです。本成果は、英国科学誌「Nature Photonics」2013年6月号(電子版: 英国時間5月12日(日)18:00)に掲載されます。なお、本研究の一部は、内閣府最先端研究開発支援プログラム(FIRSTプログラム)「量子情報処理プロジェクト」及び韓国研究財団の支援を受けて行ったものです。

今回実証に成功した方式は、光信号の量子力学的性質を保ったまま、遠く離れた地点に大きな信号として増幅して再生するもので、「量子増幅転送」と呼んでいます。
受信側にあらかじめ大きな振幅を持つ「量子重ね合わせ状態」という特殊な光を用意しておき、その一部を分岐して光回線を介して送信者へ送り共有しておきます。送信者は、この共有した光を送りたい信号と合波し、2つのビームの光子を検出して、その結果に応じて受信側で量子重ね合わせ状態を適切にフィルタリングし、信号の再生増幅を行います。
今回の実験では、高純度の量子重ね合わせ状態を生成・制御することにより、信号エネルギーの80%が失われる大きな損失を持つ光回線でも、無雑音のまま最大3倍まで増幅された信号を受信側に再生することができました。受信側で用意する量子重ね合わせ状態の振幅を更に大きくすることができれば、原理的に距離や増倍利得をいくらでも増やすことが可能です。今回の成果は、量子暗号の長距離化や量子通信の実現に大きな突破口を与えるものです。
量子増幅転送は、光を用いた量子コンピュータのゲート機能の実現や回路内での信号増幅にも利用できます。特に、光量子コンピュータを受信機に組み込めば、光子あたり最大の情報量を取り出す量子デコーダを実現できるため、本成果は、究極的な低電力・大容量の量子通信に向けた研究にも大きな進展をもたらすと期待されます。
今後、光集積化技術を用いて実験系を更に小型化し、量子暗号の長距離化や量子受信機の研究開発に適用していきます。最終的には、量子暗号、量子コンピュータ及び量子通信を光インフラの上でシステム統合するインターフェース技術の開発につなげていきます。
<掲載論文>
・掲載論文名 : Quantum tele-amplification with a continuous variable superposition state
補足資料
最新の光通信では、図1の左上部に示すように、ビット情報0、1を、山と谷が互いに反転したレーザ光の波(いわゆる2値位相変調信号)に載せて伝送します。光回線にはエネルギー損失が避けられないため、伝搬するにつれ、波の振幅は少しずつ減衰していきます。そのため、一定の区間ごとに光増幅を行うことで長距離伝送を実現します。ところが、従来の光増幅技術では、雑音の混入が原理的に避けられず、光信号の性質がどうしても劣化していきます。雑音の影響は微弱な信号ほど顕著に表れます。
今回考案した「量子増幅転送」では、微弱なレーザ光信号を、遠く離れた地点に、雑音を一切混入させることなく、大きな信号として増幅し再生することができます。従来の方法では、送りたい信号を光回線や光増幅器に次々に通していき、受信者まで届けます。しかし、量子増幅転送では従来とは全く異なる方法を用います。
まず、受信者の方で、あらかじめレーザ光の0と1の波が同時並行で存在する、量子重ね合わせ状態という特殊な光の状態(用語解説「量子重ね合わせ状態」で述べた、いわゆる「シュレーディンガーの猫状態」)を用意します。しかも、その波の振幅をできるだけ大きくなるように用意します。次に、この量子重ね合わせ状態を分波器で2つのビームB、Cに分離してから、一方のビームCを受信者から送信者へ送ります。送信者は、届いたビームCと入力信号のビームAを分波器で合波してから、2つのビームを光子検出器で測定します。ビームAのみに光子が検出され、ビームCには光子が検出されなかったときのみ、受信者側でビームBの信号を取り出すことで、無雑音のまま増幅された出力信号が受信者の手元に再生されます。
この方法では、送信者の信号そのものは光回線を通ることなく、送信者の行う光子検出の際に消えてしまいます。しかも、光子検出の結果を見ても、送りたい信号が0か1のどちらだったかは分からないようになっています。それでも、正確な入力信号が、受信者の手元へ無雑音のまま増幅された形で再生されます。
もし、受信者の用意する信号が量子重ね合わせ状態ではなく、通常のレーザ光であれば、決してこのようなことは起きません。それは、レーザ光を分波器で2つのビームに分離しても、信号転送に必要な特殊な相関現象がビーム間に形成されないためです。ところが、量子重ね合わせ状態の場合には、分波後の2つのビームB、C間には「量子もつれ状態」と呼ばれる特殊な相関が形成されます。この量子もつれ状態は、 “ビームBが0の波でビームCが1の波”と、逆に“ビームBが1の波でビームCが0の波”という2つの状態が同時並行で存在している状態です。そして、ビームCを観測して0の波だと分かれば、ビームBは自動的に1の波だと確定し、逆にビームCが1の波だと分かれば、ビームBは0の波だと確定します。このような量子もつれ状態という相関が、あらかじめ送信者と受信者間で共有されているため、受信者のビームBに入力信号を再生することが可能になります。
この操作自体は量子テレポーテーションと呼ばれる操作ですが、今回の成果では、さらに波の振幅を無雑音で増幅する機能が新たに追加されています。それを可能にしたのが、NICTで開発した高純度の量子重ね合わせ状態の生成・制御技術です。量子情報通信の研究開発では、光子一個一個を制御したり、2つの光子からなる量子もつれ状態を生成・制御する技術は多くの研究機関で開発され使えるようになっていますが、多数の光子からなる量子重ね合わせ状態の生成・制御は難易度が高く、まだ限られた研究機関でしか実現していません。今回の成果は、量子重ね合わせ状態を通信プロトコルに適用した初めてのケースになります。

量子暗号では、減衰させたレーザ光に0、1の古典ビット情報を載せて伝送します。受信者は、届いたレーザ光の中から単一光子(用語解説「光子」参照)の成分を検出して、暗号鍵を作るための光子信号を検出します。しかし、光ファイバ中での損失によって、受信者が検出できる単一光子の頻度は距離とともに減少していきます。単一光子の検出頻度が、検出器の暗計数雑音の発生頻度と同程度になると、もはや安全な暗号鍵は生成できなくなります。この距離の限界が大体100kmです。
更に長距離化するには、盗聴者がいないと仮定できる中継点を介して暗号鍵を別の暗号鍵でカプセルリレーする方法(古典カプセルリレー)や、量子中継という方法を使います。前者は、現在使われている方法ですが、中継点では量子力学を適用できず、信頼性の保証は絶対的ではありません。後者は、中継ノードでも量子力学を用いるので盗聴者がいても検知できますが、量子メモリと光子を高効率で結合させる高度な技術が必要でまだ基礎研究の段階です。
今回実証した「量子増幅転送」は、古典カプセルリレーと量子中継のちょうど中間に位置する技術で「量子リレー」と呼ばれます。本量子増幅転送の構成は、図2に示すように図1を少し拡張した形になっています。まず、送信者と受信者の間に中継ノードを用意します。次に、受信者は、「量子重ね合わせ状態」(専門的記号で|β>-|-β>)を用意してビームBとCに分岐し、「量子もつれ状態」を作ります。そして、送信者の信号(専門的記号で|α>)が中継ノードに来るのに合わせて、量子もつれ状態の片方のビームCを中継ノードに送ります。後は、図1と同様にして、中継ノードで光子検出を行い、その結果に応じた適切なフィルタリングをビームBに施して、受信者の手元にg倍に増幅した信号(専門的記号で|gα>)を再生します。
この量子リレーでは、中継ノードは盗聴者の手にあると仮定します。しかし、その場合でも、盗聴者が光子検出の結果から送信者の信号が0か1のどちらだったかを知ることはできません。送信者の信号自体も中継ノードでの光子検出の際に消えてしまいます。また、もし盗聴者が信号を勝手に作り受信者に送った場合には、量子暗号プロトコルの信号処理の段階でばれてしまう仕組みになっています。このように中継ノードに安全性の仮定を必要としません。さらに、量子メモリも不要で量子中継ほど実現が困難ではなく、現在の技術の若干の改良で伝送距離を300km圏まで延長できます。さらに、量子重ね合わせ状態の振幅を大きくとることができさえすれば、伝送距離はどこまでも延ばすことが原理的に可能です。
図3は、量子暗号の最も標準的なプロトコルであるBennett-Brassard 84方式に量子増幅転送を適用した場合の長距離化の性能予測です。計算では、現在生成可能なレベルの量子重ね合わせ状態を仮定しています。量子増幅転送によって距離が3倍以上に延長できることが分かります。
図4は、実際に行った実験結果をまとめたものです。横軸が入力信号の波の振幅αで、縦軸が出力状態の振幅α’(=gα)になります。青い直線が入力振幅を何倍に増幅して出力するかを表す利得直線です。白丸が入力振幅αと出力振幅gαのペア(α、gα)の理論上の位置を表し、赤丸が実験における入出力振幅のペアの位置を表しています。各赤丸の状態を示す青い等高線の分布図は、出力信号の波の性質を表す図です。量子力学の世界では、光の波の形状を完全に決定することは不可能で、各時刻の振幅の値は常に揺らいでいて正確には決まりません(これを不確定性原理といいます。)。各分布図は、振幅の期待値の分布とその揺らぎの広がり具合を表しています。各分布図の中の赤と青の線は、入出力状態を比較するための代表的な等高線を表しています。赤い実線が実際の入力状態、赤い点線がターゲットとなる出力状態、青い実線が実験で得られた出力状態です。各分布図の[ ]内の数字は、ターゲットと実際の出力状態間の重なり具合で、フィデリティと呼ばれ、この数字が1に近いほど、正確な量子増幅転送が行われていることを意味しています。

図4 量子増幅転送の実験結果
横軸が入力信号の波の振幅α、縦軸が出力信号の波の振幅α’(=gα)
分布図 #1~#10は、光回線のエネルギー損失が無い場合の実験データで、どの場合もフィデリティが88%~95%で、高精度の増幅転送が行われています。#11と#12は、回線損失が80%と大きい場合の実験データです。損失が80%と大きい場合でも、84%以上の高いフィデリティが達成されており、光信号に対する量子増幅転送が損失耐性を持つことを実証しています。入力振幅αをg倍に増幅転送するためには、受信端において、ターゲットの出力振幅gαと大体同程度の振幅βの持つ重ね合わせ状態を用意しておく必要があります。
現在、冷却イオン、超伝導素子、半導体素子、光回路など種々の物理系を用いて量子コンピュータの研究開発が行われています。これらの中で、光回路を用いた量子計算は、量子情報通信ネットワークを構築する上で欠かせないものです。光回路を用いた量子計算には大きく分けて2つのタイプがあります。一つは、光子一個一個で量子ビットを構成する光子量子コンピュータで、もう一つは、光子の集合体であるレーザ光の波(コヒーレント状態とも呼ばれる)で量子ビット(用語解説「量子コンピュータ」を参照)を構成するコヒーレント状態量子コンピュータです。特に、後者は、現在の光インフラにおける情報媒体であるコヒーレント状態を用いているため、光ネットワークへの応用上、極めて重要です。
今回開発した量子増幅転送は、入力信号が通常のレーザ光信号の場合のみではなく、量子ビットの場合でも増幅転送することができ、実際、コヒーレント状態に対する1ビット量子ゲート操作に相当しています。これらをさらに2つ組み合わせれば2ビットの量子ゲートが実現できます。そして、これらの基本ゲートを組み合わせることで、コヒーレント状態量子コンピュータの回路を構成することが可能になります。このように量子増幅転送は、コヒーレント状態量子コンピュータを実装する上での基本ブロックとなるものです。そして、コヒーレント状態量子コンピュータは、実際の光インフラを行き交うコヒーレント状態を処理するためにも使われ、それが次に述べるように究極的な低電力・大容量通信の実現の鍵を握っています。
究極的効率の低電力・大容量通信を実現する最適方式は、図5に示すように、送信はコヒーレント状態で符号化を行い、受信を量子デコーダで行うという方式であることが最新の理論によって示されています。量子デコーダでは、コヒーレント状態のパルス列を量子コンピュータによって処理(量子計算)してから、最後に、光子数識別によって信号判定を行います。この量子デコーダによって、古典的な通信理論の限界(シャノン限界)を打破し、現在より桁違いに小さな送信電力で大容量通信を実現できるようになります。図6に、光回線の送信電力に対する伝送速度の理論限界を示します。
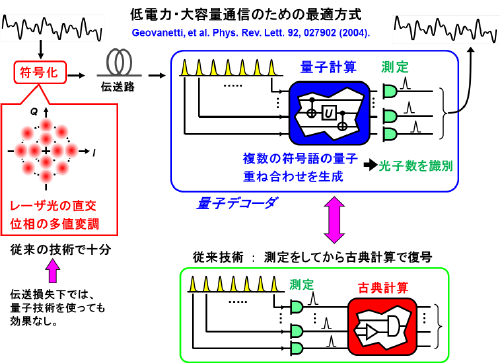

量子デコーダは、2003年にNICTによって2つの特殊な光信号パルスに対してその原理が実証されていますが、それ以降、実用的なコヒーレント状態での実現にはいまだに至っていません。実用的な量子デコーダの実現には、コヒーレント状態量子コンピュータが必要ですが、今回の成果によって、やっと1ビットの基本量子ゲートが実現できるようになった段階です。今後、量子増幅転送を2つ組み合わせることで、2ビット以上の量子ゲートを実現していく必要があります。それが実現できれば、小規模のコヒーレント状態量子コンピュータが実現でき、実用的な量子デコーダの実現が可能になります。特に、量子デコーダは、小規模であっても光通信で使われる古典デコーダの前段に組み込むことによって、通信性能を一歩一歩改善していくことが可能になるので、実用的にも重要な意味を持っています。
用語 解説
量子力学が支配するミクロな世界では、複数の異なる状態が同時並行で存在することが許される。例えば、原子の中では1個の電子が同時に複数の異なる軌道に存在できる。野球に例えると、ヒットでもあり、同時にファウルでもあるような打球を打つことが可能になる。あるいは、オーストリアの理論物理学者シュレーディンガー(1887-1961)が、量子力学の不思議さを説明する際に用いたように、一匹の猫が「生きている状態」と「死んでいる状態」に同時に存在することも原理的に可能になる(大きな系の量子重ね合わせ状態のことを“シュレーディンガーの猫状態”と呼ぶ。)。しかし、日常世界でそのような状態を実際に目にすることはない。それは、このような「量子重ね合わせ状態」は外乱によって壊れやすいため、膨大な原子や電子の固まりでできている日常スケールでは、雑音によってかき消されているためである。しかし、技術の進展によって、一個一個の粒子の量子力学の性質を直接制御できるようになり、量子重ね合わせ状態を自在に生成し制御することができるようになっている。また、最近では、複数の粒子からなる物理系でも、量子重ね合わせ状態、いわゆる“シュレーディンガーの猫状態”を生成・制御することができるようになってきた。

量子暗号は、右図に示すように、「量子鍵配送」による秘密鍵の共有と、それを用いた「ワンタイムパッド暗号化」から構成される。
量子鍵配送では、送信者が光子を変調(情報を付加)して伝送し、受信者は届いた光子一個一個の状態を検出し、盗聴の可能性のあるビットを排除(いわゆる鍵蒸留)して、絶対安全な秘密鍵(暗号化のための乱数列)を送受信者間で共有する。変調を施された光子レベルの信号は、測定操作をすると必ずその痕跡が残る(ハイゼンベルクの不確定性原理)ため、この原理を利用して盗聴を見破る。
ワンタイムパッド暗号化では、送信情報のデジタルデータを、それと同じ長さの秘密鍵(0と1のランダムなビット列)と足し算することで暗号化し、復号は更にもう一度足し算をすることで行う。パッドとは暗号鍵を意味する。一度使用した乱数列は二度と使わないというのがワンタイムパッドの規則である。ワンタイムパッド暗号は、解読が絶対的に不可能であることがシャノンにより証明されている。
従来の計算機では、1ビットにつき0か1のどちらかの値しか取り得ないので、Nビットの情報を処理する場合、全部で2N個あるビット列00…0、00…1から11…1までを一つ一つ2N回処理しなければならない。ところが、量子コンピュータでは、0でもあり同時に1でもある状態、いわゆる量子ビットを用いることで、2N個のビット列がすべて重なり合った状態を用意し、これに対して一度だけ演算することで同等の処理が実行できるため、現在のスーパーコンピュータでも不可能な超並列計算を実行することができる。
量子コンピュータを用いた新しい受信方式である量子デコーダを用いることによって、古典的な通信理論の限界(シャノン限界)を打破し、現在より桁違いに小さな送信電力で大容量通信を実現する技術。さらに、量子テレポーテーションなど、従来とは全く異なる新しい通信プロトコルなども含まれる。
量子力学に従う素粒子やその集合体が示す現象のこと。「量子」とは、それ以上分割できない計量の最小単位という意味。光も波としての性質のほかに、それ以上分割できないエネルギーの粒子、いわゆる光子としての性質を持つ。この離散性が光の代表的な量子力学的性質の一つ。この性質は光子検出器を用いることで捉えることができる。また、上記用語「量子重ね合わせ状態」も典型的な量子力学的性質の例である。2個以上の量子(光子や電子のような粒子)が、古典力学的には考えられない特殊な相関をもって結びついている状態、いわゆる「量子もつれ」も代表的な量子力学的現象である。この量子もつれ状態を構成する量子のうち、ある1つについての情報が測定によって確定すると、それに伴って別の粒子についての情報も確定する。これらの量子重ね合わせ状態や量子もつれ状態が量子情報技術の基盤となっている。
量子力学によれば、光は“波”の性質と“粒子”の性質を併せ持っている。光の粒子は「光子」と呼ばれ、これ以上分割することのできない光のエネルギーの最小単位である。例えば、光通信で通常用いられる1.5ミクロンの波長では、1光子のエネルギーは約1000京分の1(1京は1の後に0が16個ついた単位)ジュールという極めて小さな値になる。単一光子とは、パルス内に光子が一個しかない状態のことを言う。n光子状態とは、同様に、パルス内に光子がn個存在する状態のことを言う。
通信システムでは、音声や画像など送りたい情報をデジタル記号0、1の系列で表現して(いわゆる符号化して)伝送や処理を行う。符号化の際には伝送過程で起こる誤りに対抗するため、わざと余分な0、1の系列を付加して情報を表現する。例えば、0を000、1を111と3回繰り返すことで、伝送には3倍の時間がかかってしまうが、伝送の信頼性を上げることができる。つまり、000で送っても通信路での誤りによって受信側では001、010、あるいは100のような異なる系列が出る場合もあるが、0が2つ以上あれば、もともとは000だったと判断することで最終的な信号判定の誤りを減らすことができる。ここで、届いた信号を測定し、得られた0と1の系列を適切に誤り訂正処理して、実際に送られたメッセージに復元する作業を復号化、そのための復号器のことをデコーダと呼ぶ。
「量子デコーダ」とは、この復号過程に量子コンピュータを組み込んだ新しいデコーダのことである。従来のデコーダでは、まず、受信した系列の各信号パルスを測定して0、1の系列に復元してからコンピュータで誤り訂正処理を行うが、量子デコーダでは、各信号パルスを測定する前に、一旦受信した系列を量子コンピュータに入れて処理を行ってから最後に測定を行いメッセージを復元する。量子コンピュータによる処理を行うことで、従来よりも格段に高い誤り訂正を行うことができるため、より多くの情報量を取り出せるようになる。
実際、究極的効率の低電力・大容量通信を実現する最適方式は、送信はレーザ光で符号化し受信を量子デコーダで行うという方式であることが最新の理論によって示されている。これによって、古典的な通信理論の限界(シャノン限界)を打破し、現在より桁違いに小さな送信電力で大容量通信を実現できるようになる。(詳しくは補足資料の後半部分の図5、図6を参照。)
電磁波の状態の一つで、損失のある通信路を伝搬してもその雑音特性が全く変化しない状態のことを「コヒーレント状態」という。レーザ光は典型的なコヒーレント状態の一例である。
雑音の少ない電磁波同士がぶつかったときには、互いの波の山と谷の位置に応じて強めあったり弱め合ったりする。これは干渉現象と呼ばれ、干渉性をコヒーレンスと呼ぶ。コヒーレント状態は、損失のある通信路を伝搬する際、エネルギーは失われていくが、コヒーレンスは失われないため、受信側でうまく干渉を制御することで、感度の高い受信方式(コヒーレント受信方式)を構築することができる。量子力学の世界では、電磁波は波でもあり、同時に粒子としての側面を持つ。電磁波の粒子は光子と呼ばれ、1個2個と数えることができる。コヒーレント状態は、n光子状態をn=1~無限大まである係数で足し合わせたものとなっている。
本件に関する 問い合わせ先
佐々木 雅英
Tel: 042-327-6524
Fax: 042-327-6629
E-mail: 












取材依頼及び広報 問い合わせ先
廣田 幸子
Tel:042-327-6923
Fax:042-327-7587
E-mail: