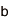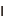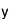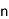独立行政法人情報通信研究機構(以下NICT)注1、国立大学法人九州大学(以下九州大学)注2、株式会社富士通研究所注3は共同で、次世代の暗号として標準化が進められているペアリング暗号について、278桁長の暗号解読に成功し、世界記録を達成しました。従来、この桁長の暗号は解読に数十万年かかることから解読不可能とされ、開発段階で利用・普及への取組が数々見られましたが、今般、新しい攻撃法の適用により148.2日間で解読できる脆弱な暗号であることが実証されました。本成果は、わが国の電子政府や国際標準化機関等において、安全な暗号技術を利用するための根拠として活用され、次世代の暗号の標準化に役立てられます。
暗号は、解読技術の進展や計算機の進歩により、解読のスピードが上がり安全性が低下するので、暗号がいつまで安全に使えるかは重要な課題です。一方で、ペアリング暗号は歴史が浅いため、新しい攻撃法に関してはその検討が未熟でした。

暗号の安全性評価の一環として、これまで解読に数十万年かかり解読不可能と考えられてきた 278桁(923ビット)のペアリング暗号について、汎用計算機21台(252コア)を用いて148.2日で解読することに成功しました。これは、情報システムにおいて、高い権限を持つ管理者になりすませることに相当します。本結果から、解読不可能と思われていた暗号が、現実的な時間内で解読できることが実証され、脆弱であることが世界で初めて示されました。
今回挑戦した問題は、従来の世界記録204桁長(676ビット)と比べ、およそ数百倍の計算パワーが必要な難問でしたが、数式を使って初期値を最適化する技術や、データ探索を二次元空間に拡張する技術などを用いた新しい攻撃法と、膨大な数値データから方程式の解を高速に計算する技術、さらには計算機が持つパワーを限界まで引き出す並列プログラミング技術などを駆使することにより、この壁を克服することができました。
今回の成果は、暗号解読の世界記録が達成されただけでなく、安全な暗号の選択や適切な鍵の交換時期を見積もるための技術的根拠となる、貴重なデータが得られたことを意味しています。安心して利用できる暗号の境界線がどこにあるのかについては、今後も引き続き研究を進めていきます。本成果は、わが国の電子政府や暗号に関する国際標準化機関等において、安全な暗号技術を利用するための根拠として活用され、次世代の暗号の標準化に役立てられます。
記載されている製品名などの固有名詞は、各社の商標又は登録商標です。
記者説明会資料
記者説明会の資料(PDF)を以下からダウンロードできます。
参考資料
ネットショッピングやネットバンキング、公的機関への電子申請など、現代の情報システムでは機密情報を扱う場面が非常に多くなっています。これらのサービスを安心して利用できるようにするためには、暗号技術による情報セキュリティの確保が欠かせません。
近年、従来の公開鍵暗号では実現困難だった利便性が高く、様々なサービスに応用可能な新しい暗号として、「ペアリング暗号」を応用した「IDベース暗号」や「検索可能暗号」、「関数型暗号」などの研究開発が盛んに行われています。一方で、ペアリング暗号はまだ歴史が浅く、安全性については検討が十分ではありませんでした。この暗号を安心して使うには、計算機の進歩などを考慮した上で、いつまで安全に利用できるかを精密に評価する必要があります。そのためには、暗号の安全性の根拠である「離散対数問題」について、解読に必要な計算資源や時間の検証・評価を理論・実験の両面から精密に行い、その結果から暗号の安全性を正確に知ることが必要です。
我々が挑戦した278桁長(923ビット)のペアリング暗号は、従来、解読不可能と考えられており、開発段階で利用・普及への取組が数々行われていました。今回解読に成功したことで、278桁長の鍵は脆弱であり、より大きな鍵を採用すべきことを意味すると同時に、解読に必要な計算資源や時間が正確に見積もられたことで、安全な暗号の選択や適切な鍵の交換時期を見積もるための技術的根拠となる、貴重なデータが得られたことを意味しています。今後、安心して使える暗号の境界値の導出については、引き続き研究を進めていく予定です。

今回の離散対数問題の解の計算では、現時点で、最も高速な手段として知られている「関数体篩(ふるい)法」をベースとして用いました。この最新の解読技術に改良を加え、さらに利用する計算機の性能を最大限活かした実装を行うことで、解読に成功しました。今回の技術の特徴は、以下のとおりです。
- 数式を使って初期値を最適化する技術
実験に先立って、解読までに必要な計算機のパワーを、理論的に見積もることができる数式を新たに提案し、数多くの初期値から、最も少ないパワーで済むと予想される初期値を選択しました。 - データ探索を二次元空間に拡張する技術
解読するには、答えの種となるデータを大量に探索する必要があります。このデータの探索に対し、従来の世界記録では「線形篩法」と呼ばれる一次元の空間を探索する手段が用いられていましたが、今回は、これを二次元空間の探索に拡張した「格子篩法」と呼ばれる方法に、更に独自に改良を施すことで、数十倍の高速化が得られました。 - 膨大な数値データから方程式の解を高速に計算する技術
膨大な数値データから導かれる巨大な方程式について、「ランチョス法」と呼ばれる方法を使って解を求めました。計算機の性能に合わせてプログラムを最適化することで、数倍の高速化が得られました。 - 計算機が持つパワーを限界まで引き出す並列プログラミング技術
最新の汎用計算機に搭載されているSIMD演算を利用し、処理の並列度を限界まで高めたプログラミングを行いました。これによりおよそ数倍の高速化が得られました。
利用した計算機はNICT、九州大学、富士通研究所のサーバ21台、252コアで、トータル148.2日間で解読に成功しました。これは、Intel Xeonプロセッサ1コアで、およそ102年の計算時間に相当します。
離散対数問題の解読は、従来から国内外のグループが挑戦してきました。下記の図は、主要なグループである「フランスの国防省及びレンヌ数学研究所のグループ」、「NICT及びはこだて未来大学」について、解読に成功したビット数を今回の結果とともに一覧にまとめたものです。縦軸は、解読する問題の難しさを数式を使って算出した値です。このように、今回我々が計算に成功した記録278桁(923ビット)は、従来の計算記録204桁(676ビット)に比べ、およそ数百倍の難しさを持つ問題であり、従来の記録を大きく上回る結果となっています。

問題の設定としては、まず、有限体![]() を
を![]() として定め、超特異楕円曲線
として定め、超特異楕円曲線![]() 上の離散対数問題から、
上の離散対数問題から、![]() ペアリングを用いて有限体
ペアリングを用いて有限体![]() 上の離散対数問題に変換したものを用います。次に、楕円曲線上の点を
上の離散対数問題に変換したものを用います。次に、楕円曲線上の点を![]() ,
,![]() とします。ただし、
とします。ただし、![]() ,
,![]() は、それぞれ円周率
は、それぞれ円周率![]() 、ならびに自然対数の底
、ならびに自然対数の底![]() を3進展開した値であり、
を3進展開した値であり、![]() は、各々楕円曲線上の点の条件を満たす最も近い値を求めたものです。これは、問題の恣意性(問題の答えが事前に分かっていることが疑われる設定)を排除するために行いました。
は、各々楕円曲線上の点の条件を満たす最も近い値を求めたものです。これは、問題の恣意性(問題の答えが事前に分かっていることが疑われる設定)を排除するために行いました。
以上の準備の下、![]() ペアリングの値を計算し、以下に示す有限体
ペアリングの値を計算し、以下に示す有限体![]() 上の離散対数問題の解読実験を実施しました。
上の離散対数問題の解読実験を実施しました。
計算機21台252コアを用い、148.2日かけて解読実験を行った結果、2012年4月24日に、以下の結果を得ることに成功しました。
組織ごとの主な役割分担は、以下のとおりです。
- NICT:計算時間短縮の理論構築・解読アルゴリズムのパラメータ最適化・計算機導入
- 九州大:プロジェクト推進管理・プログラミング・計算機管理・実験実施
- 富士通研:解読アルゴリズム設計・プログラム並列化・解読実験進捗管理

用語 解説
ペアリングと呼ばれる数式を利用することで、従来の公開鍵暗号では実現困難だった様々な利便性の高い応用が可能な次世代の暗号方式。2001年に開発された、離散対数問題を安全性の根拠とする公開鍵暗号。離散対数問題とは、与えられた数値gとaに対し、gのd乗がaと等しくなるような整数d(対数値)を求める問題。
公開鍵として受信者を一意に識別するID(メールアドレスなど)を利用可能な暗号技術。従来の公開鍵暗号と異なり、公開鍵の認証を必要としない。
データを秘匿したままキーワード検索が可能な暗号技術。
暗号化のメカニズムの中に任意の論理式を組み込むことで、暗号化並びに復号のアクセス制御ができる暗号技術。
1976年にDiffieとHellmanによって提案された暗号。暗号化に用いる鍵と復号に用いる鍵を別に用意することで、暗号化に用いる鍵を公開(公開鍵と呼ばれている)することができる。代表的な方式としてRSA暗号や楕円曲線暗号がある。
本件に関する お問い合わせ
ソフトウェアシステム研究所
セキュアコンピューティング研究部
下山武司
Tel: 044-754-2681
E-mail: 
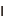





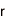
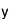













マス・フォア・インダストリ研究所
教授 高木 剛
Tel: 092-802-4456
E-mail: 


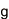



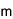


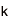
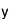










ネットワークセキュリティ研究所
セキュリティ基盤研究室
篠原直行
Tel: 042-327-5343
E-mail: 





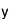

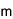
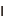

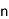








報道関係者 お問い合わせ
Tel: 03-6252-2174 (直通)
Tel: 092-642-2106
E-mail: 







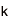
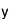

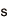
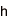









Tel: 042-327-6923
E-mail: