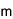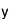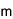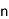現代の情報システムには、情報セキュリティの観点から様々な暗号技術が用いられています。そのため、悪意を持った攻撃者の解読能力の進歩に対して常に安全性を確保するための暗号技術の評価が必要になります。この評価において重要な役割を果たすのは、暗号技術のベースとなる数学的な問題で、その計算が、現在および将来にわたり想定しうるコンピュータの能力によっても、困難であることを確認することです。
独立行政法人情報通信研究機構(以下「NICT」という。理事長:宮原 秀夫)は、公立はこだて未来大学(学長:中島 秀之)との共同研究として、「有限体上の離散対数問題」について、これまでの世界記録を大幅に上回る676ビット長(10進数で204桁に相当)の計算に挑戦し、解読に必要なコンピュータの能力評価に初めて成功しました。公開鍵暗号では、この問題の計算が困難であることが安全性の根拠となっています。今回の成果は、現在広く利用されている1024ビット長の暗号が直ちに安全でなくなったことを示すわけではないものの、より強い暗号技術を将来導入する必要があることを示唆する結果であることから、国際標準を決定するISOや、我が国の電子政府に採用すべき暗号を推奨するCRYPTRECプロジェクトなどの場において、その導入時期を検討するための重要な技術的根拠となります。
暗号技術では、より大きな数字によって秘密情報を表現するほど安全性が向上する反面、処理性能の低下をきたすため、秘密情報を表現する適切な大きさを見積もることが重要となります。今回、我々は、今後普及が見込まれる公開鍵暗号方式のベースとなっている離散対数問題について、676ビット長の場合に、汎用コンピュータ18台で33日と、現実的な計算機環境と処理時間で計算できることを世界で初めて実証しました。本成果は、今後のコンピュータの処理能力の向上によって、現在広く使われている1024ビット長の暗号技術の安全性が2020年までに危うくなるという将来予測(CRYPTRECプロジェクトによる)で示されている経過を裏付けています。さらに、世界最長ビットに対する計算に成功したことは、我が国の暗号技術の評価能力が世界トップレベルにあることを示す結果といえます。
本成果は、公開鍵暗号に関する世界有数の国際会議であるPKC2010(5月26日?28日:パリ)で発表する予定です。また、CRYPTRECプロジェクトに報告し、CRYPTRECシンポジウム2010(3月2日~3日:東京)で紹介いたします。我々は今後も、安全な暗号利用を促進するための指針を提供するため、より精密な評価を実施してまいります。
ネットショッピングやネットバンキングなど、現代の情報システムでは機密情報を扱う場面が非常に多くなっています。そのため、様々な暗号技術を利用して情報セキュリティを十分に確保する必要があります
近年、従来の公開鍵暗号では実現困難だった、利便性が高く様々なサービスに応用可能なIDベース暗号などの基礎となる「ペアリング暗号」の研究が盛んに行われています。NICTと公立はこだて未来大学は、ペアリング暗号の安全性について共同研究を行ってきました。
ペアリング暗号は「有限体上の離散対数問題」の難しさを安全性の根拠としているため、安全性を正確に評価するためには、計算可能なビット数の検証・評価を行う必要があります。今回、我々が676ビットの計算に成功したことは、広く扱われている1000ビット程度の計算が、近い将来に可能になってしまう可能性を示唆しており、従ってより長いビット数に変更したペアリング暗号を採用すべき時期を見積るための技術的根拠となります。
有限体上の離散対数問題の計算は、従来から世界各国の様々なグループが挑戦してきました。主要なグループである、(1)「ドイツのボン大学数学研究所のグループ」、(2)「フランスの国防省およびレンヌ数学研究所のグループ」、そして(3)「NICTおよび公立はこだて未来大学」について、計算に成功したビット数を比較すると以下のようになります。このように、今回我々が計算に成功したビット数(676ビット)は、従来の計算記録(613ビット)を大きく上回る結果となっています。

以下、今回の計算におけるそれぞれのステップの詳細を示します。
- 多項式選択
このステップは残りのステップの計算量を決める重要なステップですが、効率的な選択手法が提案されているため、計算をほとんど必要としません。今回は、特に有効であると考えられている二つの選択手法について比較実験を行い、後のステップの計算がより少ないと予想される選択手法を用いました。 - 関係探索
このステップは、4ステップ中最も多くの計算が必要となりますが、ほとんど通信を行わずに並列計算が可能であるため、多くの計算機を利用することでより高速に計算を行うことができます。今回の計算では、扱った問題の数学的構造を利用することでこのステップの計算を従来のおよそ8倍高速に行うことができました。このステップでは、計算に約18日かかりました。 - 線形代数計算(連立方程式の解法)
このステップも関係探索と同様に多くの計算を必要とするステップですが、並列計算を行う際には通信を行う必要があるため、単純に多くの計算機を利用するだけでは高速に計算を行うことができません。今回は、扱った問題特有の数学的構造を利用することで、このステップの計算を従来のおよそ36倍の高速に行うことに成功しました。これにより、従来は関係探索と同程度の計算が必要だったこのステップを、およそ12時間の計算で行うことができました。 - 離散対数計算(連立方程式の解を用いた任意の元の離散対数の計算)
この最後のステップでは、関係探索と同様の計算を行いますが、関係探索と比較すると計算量はさほど必要とはしません。公立はこだて未来大学のサーバ6台のみを利用し、14日かけて、解となる離散対数を計算することに成功しました。得られた解について以下に詳述します。

用語解説
有限体とは、有限個の要素に対して四則演算を行うことができる集合であり、公開鍵暗号やIDベース暗号を構成する上での基本的数学構造である。今回の解読対象となる有限体はGF(3^6・71)と表記され、その有限体の元は70次の多項式として表現される。離散対数問題とは、有限体の元g(x)とa(x)に対し、g(x)^l = a(x)を満たす整数lを求める問題。有限体上の離散対数問題が計算困難であることが、公開鍵暗号やIDベース暗号の安全性の根拠となっている。
1976年にDiffieとHellmanによって提案された。従来の暗号では、暗号化と復号に用いる鍵が同一であるため、送信者と受信者の間で鍵を共有する必要があったが、公開鍵暗号では暗号化に用いる鍵と復号に用いる鍵を別個に用意することで、暗号化に用いる鍵を公開することができ、同じ鍵を共有する必要が無い。
電子政府で利用が推奨される暗号技術(電子政府推奨暗号)を決定するために、暗号技術の評価と安全性の監視、暗号技術の適切な実装法・運用法の検討を行うプロジェクト。総務省及び経済産業省が共同で運営する暗号技術検討会と、技術的検討を行う3つの委員会(暗号方式委員会、暗号実装委員会、暗号運用委員会)で構成される。
1984年にShamirが概念を提案した後に、境、大岸、笠原とBoneh、Franklinによって実用的な方式が提案された公開鍵暗号の一種。公開鍵として受信者を一意に識別するIDを利用できるため、公開鍵の認証を必要とせず、従来の公開鍵暗号に比べて利便性が高い。
1994年にAdlemanによって提案された、有限体上の離散対数問題の計算アルゴリズム。標数の小さな有限体に対しては漸近的に最も高速なアルゴリズムとして知られている。しかし、現在知られている評価は漸近的なものであるため、具体的な問題に対する実際の計算時間を正確に見積もるためには、計算機による大規模計算実験を行う必要がある。
情報通信セキュリティ研究センターセキュリティ基盤グループ
松尾 真一郎
Tel:042-327-5782
E-mail: 













システム情報科学部情報アーキテクチャ学科
高木 剛
Tel:0138-34-6224
E-mail: 












報道担当 廣田 幸子
Tel:042-327-6923
E-mail: 

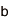
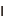




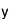

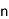








共同研究センター宮嶋 克己
Tel:0138-34-6571
E-mail: