1. Home>
  2. Publicity>
  3. Press Release>
  4. 2024>
  5. Developed Compiler Acceleration Technology for Quantum Computers
日本語
Print

Developed Compiler Acceleration Technology for Quantum Computers

- Probabilistic method reduces optimal gate sequence search time by orders of magnitude -
May 9, 2024

National Institute of Information and Communications Technology
Tokyo University of Science
School of Science, The University of Tokyo

Highlights

  • Developed a new compilation method to generate optimal sequences to be executed on quantum computers
  • The new method is based on a probabilistic approach and reduces the time to search for the optimal sequence by several orders of magnitude.
  • Expected to contribute to quantum information processing at quantum nodes that support the quantum internet

Abstract

The National Institute of Information and Communications Technology (NICT, President: TOKUDA Hideyuki, Ph.D.), RIKEN (President: GONOKAMI Makoto, Ph.D.), Tokyo University of Science (President: Dr.  ISHIKAWA Masatoshi), and the University of Tokyo (President: FUJII Teruo, Ph.D.) succeeded in developing a technique to quickly search for the optimal quantum gate sequence for a quantum computer using a probabilistic method.
To make a quantum computer perform a task, it must use a compiler to convert instructions written in a programming language into a sequence of gate operations on quantum bits, or qubits for short. We previously applied optimal control theory (GRAPE algorithm) to an exhaustive search to develop a method to identify the theoretically optimal gate sequence, but as the number of qubits increases, the number of possible combinations increases. As the number increases explosively, an exhaustive search becomes impossible. For example, if we were to perform an exhaustive search to find the optimal gate sequence for the task of generating an arbitrary quantum state of 6 qubits, it would take longer than the age of the universe using the fastest classical computer currently available.
Therefore, we attempted to develop a method to search for the optimal quantum gate sequence using a probabilistic approach and succeeded. Using the supercomputer Fugaku, it was confirmed and demonstrated that using a new probabilistic random search method, it is possible to search for the optimal quantum gate sequence for the above problem in a few hours.
This new method is expected to speed up quantum computer compilers, become a useful tool for practical quantum computers, and lead to improved performance of quantum computer devices. It can also be applied to optimize quantum information processing at quantum relay nodes, so it is expected to contribute to the realization of the quantum Internet and the reduction of environmental impact.
This result was published in the American scientific journal "Physical Review A" on May 6, 2024.

Background

Quantum computers, which are currently under development, are expected to have a major impact on society. Their benefits include reducing the environmental burden by reducing energy consumption, finding new chemical substances for medical use, accelerating the search for materials for a cleaner environment, etc. One of the big problems for quantum computers is that the quantum state is very sensitive to noise, so it is difficult to maintain it stably for a long time (maintaining a coherent quantum state).
For best performance, operations must proceed within a time that allows the quantum state to remain coherent. However, apart from the special case where the number of qubits is very small, no good method has been known to find the optimal quantum gate sequence. A solution that avoids the difficulty of the explosive increase in the number of possible gate sequences even in large-scale quantum computations and allows efficient searches within the time and computational resources that can be performed on classical computers has been awaited.

Achievements

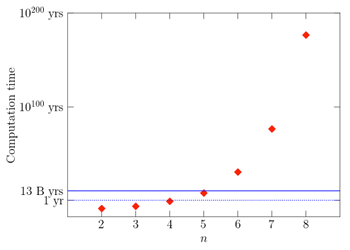
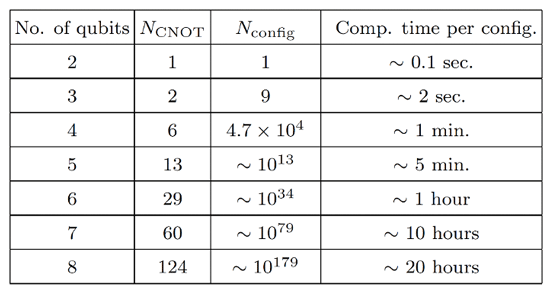
Figure 1 Estimated calculation time when performing a search to optimize the fidelity F for every gate arrangement using GRAPE to prepare the state of n qubits. The solid blue line is the time from the beginning of the universe to the present (13.7 billion years).
[Click picture to enlarge]

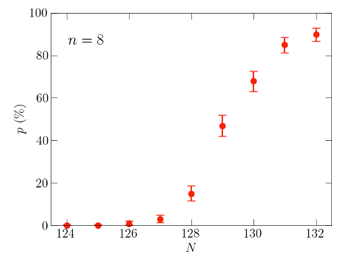
Figure 2 The appearance rate of optimal quantum sequences with F=1 calculated using the supercomputer Fugaku. N is the number of 2-qubit gates used for state preparation (green vertical line in Figure 4 in the Glossary). This figure is for the case of n=8 qubits. The appearance rate of F=1 at values of N that slightly exceed the theoretical lower bound of N=124 increase rapidly.
[Click picture to enlarge]
The research team introduced a probabilistic method to develop a systematic method that can efficiently search for the optimal quantum gate sequence within the execution time and computational resources.
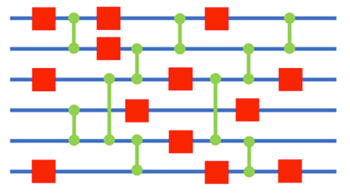
When a computer stores and processes information, all information is converted to a string of bits with values of 0 or 1. A quantum gate sequence is a computer program written in a human-readable language after it has been converted so that it can be processed by a quantum computer (see Figure 4 in the Glossary). The quantum gate sequence consists of 1-qubit gates and 2-qubit gates. The best sequence is the one with the fewest gates and shows the best performance (the number of red squares and green vertical lines is the smallest in Figure 4 in the Glossary).
Figure 1 shows the estimated calculation time when a search is performed to optimize the fidelity F on the fastest classical computer for every gate arrangement using the optimal control theory algorithm GRAPE for preparing n qubit states. The solid blue line is the so-called age of the universe (13.7 billion years). As the number of qubits increases, the number of possible combinations increases explosively, so at n=6, the total calculation time exceeds the age of the universe.
Analysis of all possible sequences for small qubit numbers reveals that there are many optimal quantum gate sequences (shown in Figure 5 in the Appendix). This suggests the possibility of expanding to large quantum tasks and finding the optimal quantum gate sequence using a probabilistic search method rather than an exhaustive search.
Figure 2 shows the appearance rate (p) of sequences with fidelity F=1 for the preparation of a state consisting of n=8 qubits, which was investigated using the supercomputer Fugaku. The rate p is expressed as a function of the number of 2-qubit CNOT gates (N) in the sequence. It is clear that the probabilistic method is very efficient because the F=1 occurrence rate increases rapidly when the lower limit of N (N=124) is exceeded. For example, the appearance rate of F=1 at N=129, which is a little over N=124, is over 50%, so if you search for a gate arrangement twice, you will find a quantum sequence that has F=1 at least once on average (see Table 1 in the Appendix). In this way, it has been found that by using a probabilistic method, it is possible to search for optimal quantum gate sequences several orders of magnitude faster than when searching using an exhaustive search method.

Future prospects

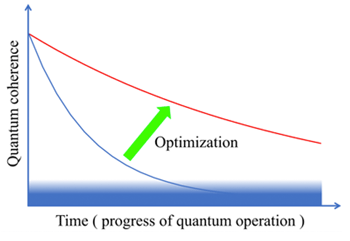
Figure 3 Improving quantum computer performance (conceptual diagram). Quantum computer coherence declines over time. If the coherence gets too low, the information in the quantum computer becomes meaningless. By optimizing the operation of quantum computers, more information can be processed before quantum coherence falls below the utility threshold.
[Click picture to enlarge]

The developed systematic and probabilistic method to provide optimal quantum gate sequences for quantum computers is expected to become a useful tool for practical quantum computers and speed up quantum computer compilers. It is expected to improve the performance of quantum computing devices (see Figure 3) and contribute to the development of quantum nodes in the quantum internet and the reduction of environmental burden.
In the future, the research team will integrate the results obtained in this study with machine learning approaches and apply them to optimize the performance of quantum computers, aiming to further speed up quantum compilers and create a database of optimal quantum gate sequences.

Role of each organization

  • National Institute of Information and Communications Technology: Research concept, analysis using GRAPE algorithm including probabilistic approach, Discussion on analysis of results and interpretation, paper writing
  • RIKEN: Creation and analysis of program code for implementation of the supercomputer Fugaku, Discussion on analysis of results and interpretation, paper refinement
  • Tokyo University of Science: Concept and discussion of research, paper refinement
  • The University of Tokyo: Research concept, Discussion on analysis of results and interpretation, paper refinement

Article information

Journal: Physical Review A
DOI: 10.1103/PhysRevA.109.052605
URL: https://link.aps.org/doi/10.1103/PhysRevA.109.052605
Title: Quantum circuit synthesis via a random combinatorial search
Authors: Sahel Ashhab, Fumiki Yoshihara, Miwako Tsuji, Mitsuhisa Sato, and Kouichi Semba

Part of this research is supported by the Ministry of Education, Culture, Sports, Science and Technology Optical and Quantum Leap Flagship Program (Q-LEAP) “Quantum Software Research and Development and Application by Intelligent Quantum Design” (JPMXS0120319794) and by the Center of Innovations for Sustainable Quantum AI (SQAI) (JST Grant Number JPMJPF2221). The research used computational resources of the supercomputer Fugaku provided by the RIKEN Center for Computational Science.

Appendix

Regarding the effectiveness of the newly developed probabilistic search method

A previous approach analyzed all possible sequences of basic quantum gates and used a computational algorithm called GRAPE, a numerical optimal control theory algorithm, to find the optimal parameters needed for each quantum gate sequence. Figure 5 shows the data that served as the starting point for this research. In the case of this task, if the number N of two-qubit gate operations used is less than 6, there is no sequence that can achieve fidelity F=1, and the proportion of approximate solutions decreases as the fidelity approaches F=1. In the case of N=6, a sequence that can achieve fidelity F=1 appears for the first time, and the proportion of gate sequences that have F=1 is as much as 20% of all possible gate sequences (peak at the right end 1-F=10－12 in Figure 5).
Figure 5 Histogram of fidelity F values for all possible CNOT gate configurations for one instance of a quantum state preparation task consisting of four qubits. A logarithmic scale is used on the x-axis to magnify the region close to F=1 and make it easier to identify the histogram in this region. The dotted line (blue), dashed line (green), and solid line (red) correspond to the number of 2-qubit gate operations with N =4, 5, and 6, respectively. The peak at 1−F=10－12 includes all configurations that gave 1−F<10－12, and it contains about 20% of all possible configurations.


Table 1 shows the system size of the quantum circuit, the total number of possible gate configurations, and the computation time for each configuration for the task of quantum state preparation in the n-qubit system explored in this research.

Table 1 Comparison of estimates for the total number of possible gate configurations, and computation time per configuration as functions of system size. The computation time values in this table are specific to our computing resources. Each calculation was performed on one CPU core up to n=4, and on approximately 10 CPU cores for n≥5. Calculations up to n ≤ 7 were performed on a workstation, and calculations for n = 8 were performed on the supercomputer Fugaku. In the table, "NCNOT" means the theoretical minimum for the number of CNOT gates required to obtain fidelity F=1.

Glossary

Figure 4 Quantum gate sequence (conceptual diagram)

Quantum gate sequence

A set of instructions that specify the steps for gate operations to be performed on multiple qubits. In Figure 4, the six horizontal blue lines represent six qubits, with the input on the left and the output on the right. Operations are executed from left to right. Each red square represents a 1-qubit gate, and each green vertical line connecting two blue lines represents a 2-qubit gate. A quantum gate sequence consists of a sequence of 1-qubit gates and 2-qubit gates, but the optimal sequence is the one that achieves high performance with the smallest number of gates.


Probabilistic approach

A computational method that randomly tries possible solutions and may succeed or fail. If there are many solutions, probabilistic methods may perform better than methods that analyze all possible solutions.


Gate

A simple operation performed on one or two bits of information. Several recent studies have proposed improved methods (recipes) for constructing sequences of quantum gates that perform various quantum tasks. However, these recipes do not necessarily yield the shortest sequence of quantum gates.


GRAPE

The abbreviation of GRadient Ascent Pulse Engineering. A numerical algorithm that uses the principles of optimal control theory to find the optimal pulse to control a quantum system.


Developed a method of applying optimal control theory (GRAPE algorithm) to an exhaustive search to identify the theoretically optimal gate sequence.

Press Release dated September 2, 2022,
“New Method to Systematically Find Optimal Quantum Operation Sequences for Quantum Computers Developed”
https://www.nict.go.jp/en/press/2022/09/02-1.html


Fidelity

A measure of the "closeness" of two quantum states. It represents the probability that one quantum state passes the test of being identified as another quantum state. If two quantum states are identical, the fidelity between them is equal to 1 (F=1). The fidelity has also been generalized for use as a measure of "closeness" between two unitary operators.


Theoretical lower bound that gives F=1

The minimum number of CNOT gates required in a quantum gate sequence to obtain fidelity F=1. In the case of n-qubit state preparation, as the number of qubits (n) increases, the number of representable state parameters also increases, as shown in the "Number of CNOT gates (NCNOT)" column in Table 1 of the Appendix.
The CNOT gate is a type of two-qubit gate. It serves to flip the state of the second qubit (target qubit) if and only if the first qubit (control qubit) is |1>.


Quantum coherence

A number between 0 and 1 that represents how much the quantum information has been degraded by device noise or other imperfections. The quantum coherence index equals 1 when the information is first input into the quantum processor and is still intact. If the quantum coherence index is equal to zero, it means that the original information is completely lost.
One of the biggest issues that need to be addressed in the further development of quantum computers is how to cope with the gradual loss of information (the inability to maintain a coherent quantum state) caused by the noise inside the computer.

Technical Contact

ASHHAB Sahel
Quantum ICT Laboratory
Koganei Frontier Research Center
Advanced ICT Research Institute
National Institute of Information and Communications Technology


YOSHIHARA Fumiki
Department of Physics, Faculty of Science Division 1
Tokyo University of Science


SEMBA Kouichi
Institute for Photon Science and Technology
Faculty of Science, Graduate School of Science,
The University of Tokyo

Media Contact

Press Office, Public Relations Department
National Institute of Information and Communications Technology


Public Relations Section
Tokyo University of Science


Office of Communication
School of Science, The University of Tokyo