1. Home>
  2. Publicity>
  3. Press Release>
  4. 2022>
  5. New Method to Systematically Find Optimal Quantum Operation Sequences for Quantum Computers Developed
Print
日本語

New Method to Systematically Find Optimal Quantum Operation Sequences for Quantum Computers Developed

September 2, 2022

National Institute of Information and Communications Technology
Keio University
Tokyo University of Science
School of Science, The University of Tokyo

Highlights

  • Developed a new method for finding optimal quantum operation sequences for quantum computers
  • Based on GRAPE, the new method systematically finds quantum operation sequences and enables efficient task execution
  • Expected to contribute to improving the performance of quantum computers and reducing environmental impact

Abstract

The National Institute of Information and Communications Technology (NICT, President: TOKUDA Hideyuki, Ph.D.), Keio University (President: ITOH Kohei, Ph.D.), Tokyo University of Science (President: Dr. ISHIKAWA Masatoshi), The University of Tokyo (President: Dr. FUJII Teruo), succeeded for the first time in developing a method for systematically finding the optimal quantum operation sequence for a quantum computer.
In order for a quantum computer to perform a task, we need to write a sequence of quantum operations. Until now, computer operators have written their own quantum operation sequences based on existing methods (recipes). What we have developed this time is a systematic method that applies optimal control theory (GRAPE algorithm) to identify the theoretically optimal sequence from among all conceivable quantum operation sequences.
This method is expected to become a useful tool for medium-scale quantum computers and is expected to contribute to improving the performance of quantum computers and reducing environmental impact in the near future.
This result was published in the American scientific journal "Physical Review A" on August 23, 2022.

Background

Figure 1 Quantum operation sequence
(conceptual diagram)
The six horizontal blue lines represent six qubits, with the input on the left and the output on the right. Operations are executed from left to right. Each red square represents a 1-qubit operation, and each green vertical line connecting two blue lines represents a 2-qubit operation. The optimal quantum operation sequence is realized with the fewest operations.

Quantum computers, which are currently under development, are expected to have a major impact on society. Their benefits include reducing the environmental burden by reducing energy consumption, finding new chemical substances for medical use, accelerating the search for materials for a cleaner environment, etc.
One of the big problems for quantum computers is that the quantum state is very sensitive to noise, so it is difficult to maintain it stably for a long time (maintaining a coherent quantum state). In order to obtain the best performance, it is necessary to complete the operations within the time that the coherent quantum state is maintained. There was a need for a method to systematically identify the optimal sequences.

Achievements

Figure 2 The maximum fidelity F that can be achieved when preparing four-qubit states
N is the number of 2-qubit gates used for state preparation (the green vertical line in Figure 1), F is the fidelity (if less than 1, the target state preparation is incomplete), and n is the number of qubits.

The research team has developed a systematic method to identify the optimal quantum operation sequence.
When a computer stores and processes information, all information is converted to a string of bits with values of 0 or 1. A quantum operation sequence is a computer program written in a human-readable language that is converted so that it can be processed by a quantum computer (see Figure 1). The quantum operation sequence consists of 1-qubit operations and 2-qubit operations. The best sequence is the one with the fewest operations and shows the best performance (the number of red squares and green vertical lines is the smallest).
The new method analyzes all possible sequences of elementary quantum operations using a computational algorithm called GRAPE, a numerical optimal control theory algorithm. Specifically, we create a table of quantum operation sequences and the performance index (fidelity F) for each sequence, ranging from thousands to millions, depending on the number of qubits and the number of operations under investigation. The optimal quantum operation sequence is systematically identified based on the accumulated data. Figure 2 shows the relationship between the length of the quantum operation sequence and its performance index, and it can be seen that if the number of qubits n is 4, five or more 2-qubit gates are required.
It is also possible for the new method to analyze the complete list of all quantum operation sequences and evaluate conventional recipes. As such, it can provide a valuable tool for establishing benchmarks for past and future research on the performance of few-qubit quantum algorithms.

Future prospects

Figure 3 Improving quantum computer performance (conceptual diagram)
Quantum computer coherence declines over time. If the coherence gets too low, the information in the quantum computer becomes meaningless. By optimizing the operation of quantum computers, more information can be processed before quantum coherence falls below the utility threshold.

The systematic method to find the optimal quantum operation sequence for quantum computers is expected to become a useful tool for medium-scale quantum computers. In the near future, it is expected to improve the performance of quantum computers (see Figure 3) and contribute to reducing the burden on the environment.
We also found that there are many optimal sequences of quantum operations that are excellent (see Appendix for details). This means that a probabilistic approach could extend the applicability of this new method to larger tasks. Approaches based on analyzing large datasets suggest the possibility of integrating machine learning with our new method to further enhance the predictive power. In the future, the research team will apply the results obtained this time to the optimization of tasks obtained from actual quantum algorithms.

Role of each organization

- National Institute of Information and Communications Technology:
Research concept, analysis using GRAPE algorithm, paper writing
- Keio University: Concept and discussion of research, paper refinement
- Tokyo University of Science: Discussion on analysis of results and interpretation, paper refinement
- The University of Tokyo: Discussion on analysis of results and interpretation, paper refinement

Article information

Journal: Physical Review A
DOI: 10.1103/PhysRevA.106.022426
Title: Numerical analysis of quantum circuits for state preparation and unitary operator synthesis
Authors: Sahel Ashhab, Naoki Yamamoto, Fumiki Yoshihara, and Kouichi Semba

Appendix

Details of this achievement

The new method analyzes all possible sequences of elementary quantum operations and uses a computational algorithm called GRAPE, a numerical optimal control theory algorithm, to find the optimal parameters required for each sequence of quantum operations. In this way a table of quantum operation sequences and their performance indicators is created. The size of each such table ranges from thousands to millions, depending on the number of qubits and the number of operations under investigation. Based on the accumulated data, the optimal quantum operation sequence is identified (see Figure 4).
In addition to identifying the optimal quantum operation sequence, several other results were obtained using the new technique. It turns out that even for relatively short sequences of quantum operations, there are usually many different ways to perform quantum tasks with the same efficiency. It is not possible to obtain this result with conventional methods of finding one way to perform a desired task.

Figure 4 The maximum achievable fidelity F for preparing n-qubit quantum states as a function of the number of two-qubit gates N
The ○ at (N=1, F=1) represents the fact that one 2-qubit gate (N=1) is enough to completely prepare an arbitrary state of two qubits. The ✕ at (N=3, F=1) represents the fact that three qubits require three 2-qubit gates.
The ● at (N=6, F=1) represents a new finding that six 2-qubit gates are required to completely prepare an arbitrary state of four qubits. The ● near (N=5, F=1) represents that an arbitrary state of four qubits can be prepared with very high fidelity by five 2-qubit gates.


Another result obtained in this work is that high efficiencies may be achieved using short sequences of quantum operations that were believed to be too short to complete the desired task. (See the ● near (N=5, F=1) in Figure 4). From a practical application point of view, it may be desirable to use such a short sequence of quantum operations given all other noise and imperfections of the device (see Figure 5).

Figure 5 Comparing quantum operation sequences performing the same quantum task in information-loss environments
Information is slowly lost due to noise and imperfections in quantum computers. Long sequences of quantum operations can render the computation useless because the original information is lost before the computation is completed. In this case, optimizing the operation can make a dramatic difference in a computer's ability to successfully complete a computation. The difference between non-optimized and optimized sequences increases as the computer size increases. As a result, optimizing the sequence of quantum operations can improve the efficiency of quantum computers by orders of magnitude. Red squares and green lines represent 1-qubit operations and 2-qubit operations, respectively, as in Figure 1. The lightning bolt symbol indicates noise that causes information loss.

Glossary

Quantum computer

A computer that makes use of quantum superposition, entanglement, and other natural abilities that conventional classical computers have not been able to use, and that can perform calculations orders of magnitude faster using completely new methods. In 2019, Professor John Martinis (then at Google) and his team demonstrated quantum supremacy (that quantum computers can solve problems that no classical computer can solve in a practical amount of time) using a 53-qubit superconducting quantum processor.
Recently, a few research teams around the world built quantum computers containing tens of qubits. Currently, IBM's Eagle processor is the largest quantum computer with 127 qubits. Processors of this size (tens or few hundreds of qubits) are called medium-scale quantum computers.


GRAPE

The abbreviation of GRadient Ascent Pulse Engineering. A numerical algorithm that uses the principles of optimal control theory to find the optimal pulse to control a quantum system in a specified way.


Gate

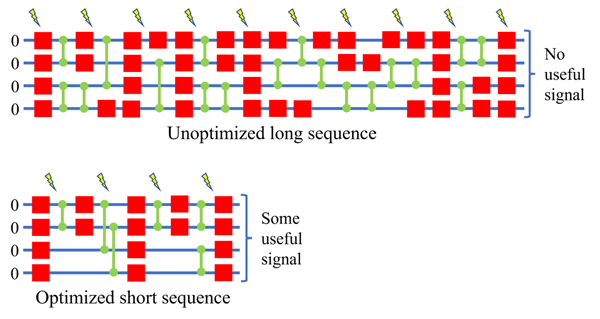
A simple operation performed on one or two bits of information. Several recent studies have proposed improved methods (recipes) for constructing sequences of quantum operations that perform various quantum tasks. However, these recipes do not necessarily yield the shortest sequence of quantum operations.


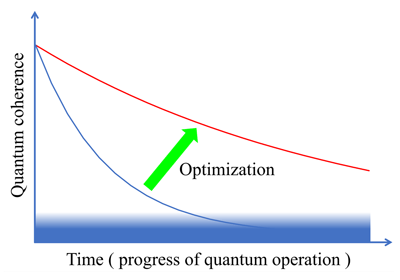
Quantum coherence

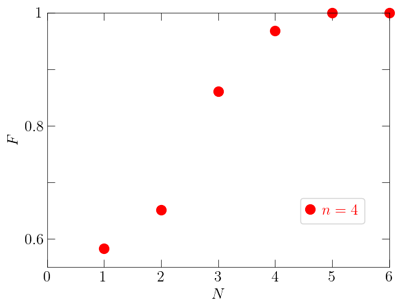
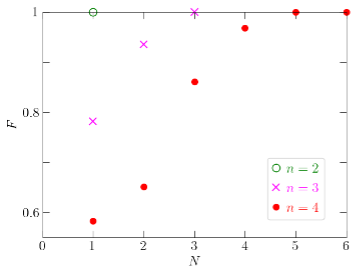
A number between 0 and 1 that represents how much the quantum information has been degraded by device noise or other imperfections. The quantum coherence index equals 1 when the information is first input into the quantum processor and is still intact. If the quantum coherence index is equal to zero, it means that the original information is completely lost.
One of the biggest issues that need to be addressed in the further development of quantum computers is how to cope with the gradual loss of information (the inability to maintain a coherent quantum state) caused by the noise inside the computer.


Probabilistic approach

A computational method that randomly tries possible solutions and may succeed or fail. If there are many solutions, probabilistic methods may perform better than methods that analyze all possible solutions.


Part of this research is supported by the Ministry of Education, Culture, Sports, Science and Technology Optical and Quantum Leap Flagship Program (Q-LEAP) “Quantum Software Research and Development and Application by Intelligent Quantum Design” (JPMXS0120319794, Research Director: FUJII Keisuke) and Science and Technology Supported by Japan Science and Technology Agency (JST) CREST "Creation and Control of Superconducting Quantum Metamaterials" (JPMJCR1775, Principal Investigator: SEMBA Kouichi).

Technical Contact

ASHHAB Sahel
Quantum ICT Laboratory
Koganei Frontier Research Center
Advanced ICT Research Institute
National Institute of Information and Communications Technology

YAMAMOTO Naoki
Department of Applied Physics and Physico-Informatics
Faculty of Science and Technology
Keio University

YOSHIHARA Fumiki
Department of Physics, Faculty of Science
Tokyo University of Science

SEMBA Kouichi
Institute for Photon Science and Technology
Faculty of Science, Graduate School of Science,
The University of Tokyo

Media Contact

Press Office
Public Relations Department
National Institute of Information and Communications Technology

Office of Communications and Public Relations
Keio University

Public Relations Division
Tokyo University of Science

Office of Communication
School of Science, The University of Tokyo